Sort Linked List using Merge Sort.
Given a Linked list, Sort it using Merge Sort Algorithm.
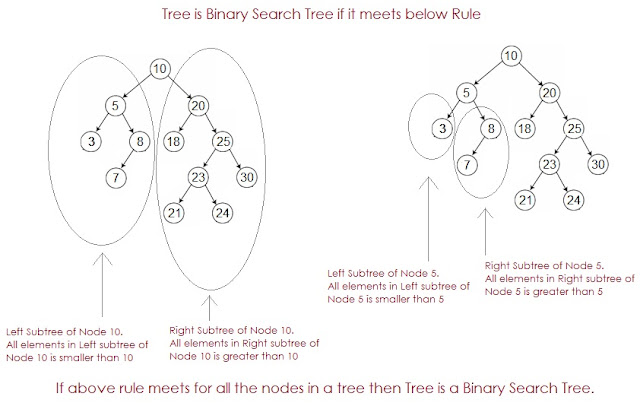
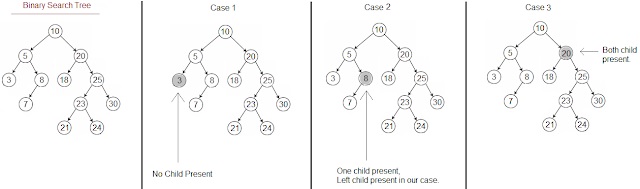
Merge sort is preferred algorithm for sorting a linked list, lets see why,
The way linked list is structured which doesn't allow random access makes some other algorithms like Quicksort perform poorly, So Merge sort is often preferred algorithm for sorting linked list.
Lets understand what is the input and the expected output.