How to construct a Binary Tree from given In order and Level order traversals.
Let us first understand what we want to achieve? what is the input and what will be the expected output?
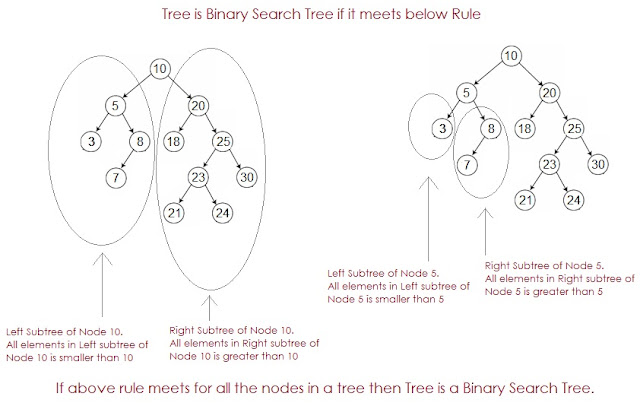
Question:
Two traversals are given as input,
int[] inOrder = { 4, 2, 6, 5, 7, 1, 3 };
int[] levelOrder = { 1, 2, 3, 4, 5, 6, 7 };
By using above 2 given In order and Level Order traversal, construct Binary Tree like shown below,